Dynamic Programming

状态定义? 状态转移方程?

启发思路: 选或不选 / 选哪个

DP 萌新三步:

1. 思考回溯要怎么写

1.1 入参和返回值

1.2 递归到哪里

1.3 递归边界和入口

2. 改成记忆化搜索

3. 1:1 翻译成递推

Step1: Understand the problem.

Cleary identiy the problem's input and output and determine what you're aiming to achieve

Step2: Define the State.

Decide on the state representation, usually in the form of an array or matrix. The state should capture the subproblem at any given point. For example. dp[i] can represent the optimal solution at the i-th step

Step3: State Transition Equation

Develop the rule that relates one state to another. This step is crucial and involves finding how a solution to one subproblem can be derived from other subproblems. For example, in the Fibonacci sequence, the state transistion equation is \(dp[i] = dp[i - 1] + dp[i - 2]\).

Step4: Initialization

Set up the base case or initial values for the state array, typically based on the simplest or smallest subproblems. For example, in the Fibonacci sequence, initialize with \(dp[0] = 0\) and \(dp[1] = 1\).

Step5: Determine the Computation Order

Decide the order in which to compute the state values, usually from smaller to larger subproblems, ensuring that each state's dependencies are already calcuated.

Step6: Handle Edge Cases

Consider any boundary conditions or special cases, such as out-of-bounds indices or unique input values.

Step7: Return the Result:

Finally, return the solution from the state array based on the problem's requirements.

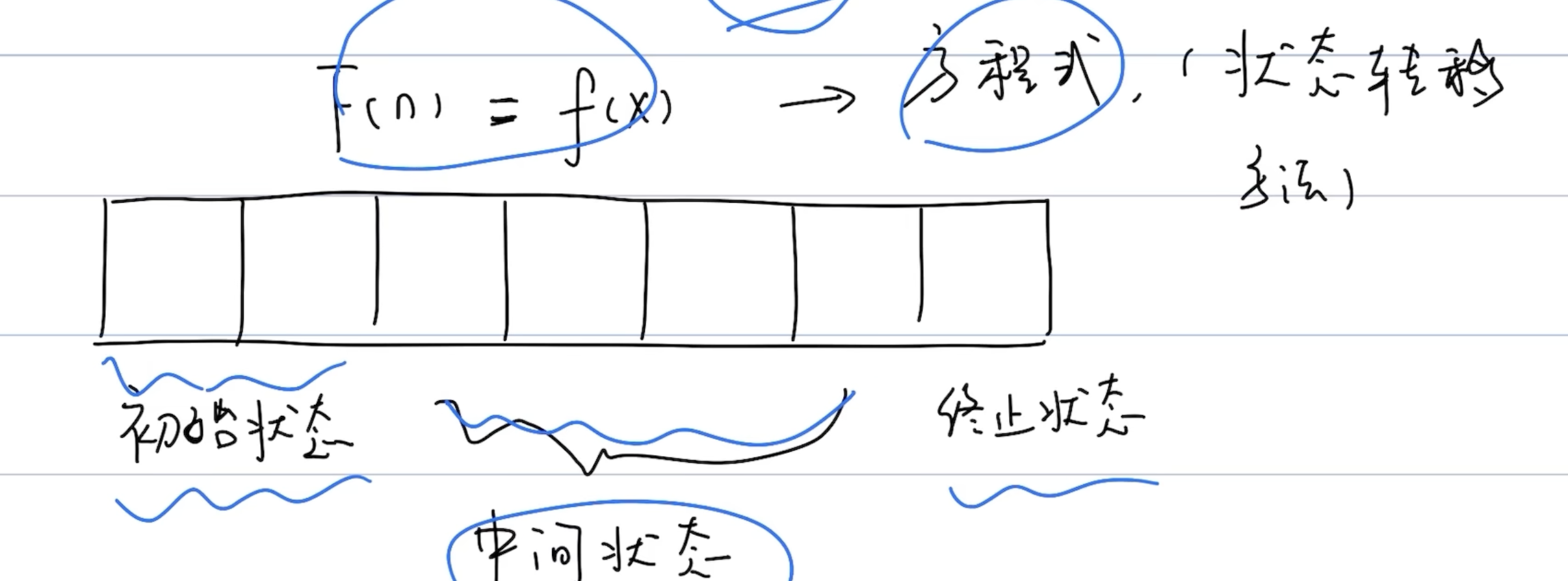
状态转移: 使用历史的记录状态来获取当前的状态 转移到当前了

一般状态用 1D array 或者 2D array 来存

动态规划能干些什么

1. 计数:有多少种方法|方式 - 62. Unique Paths
2. 求最值: 最大值 | 最小值 - 53. Maximum Subarray
3. 求存在性: 是否存在某个可能; 是否存在 - 是否存在机器人从左到右的路径

5. Longest Palindromic Substring

62. Unique Paths

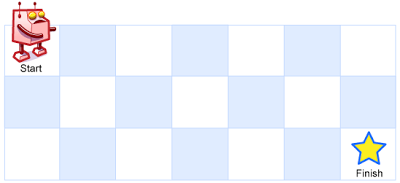
There is a robot on an m x n grid. The robot is initially located at the top-left corner (i.e., grid[0][0]). The robot tries to move to the bottom-right corner (i.e., grid[m - 1][n - 1]). The robot can only move either down or right at any point in time.

Given the two integers m and n, return the number of possible unique paths that the robot can take to reach the bottom-right corner.

The test cases are generated so that the answer will be less than or equal to 2 * 109.

Example 1:

Input: m = 3, n = 7
Output: 28

Example 2:

Input: m = 3, n = 2
Output: 3
Explanation: From the top-left corner, there are a total of 3 ways to reach the bottom-right corner:
1. Right -> Down -> Down
2. Down -> Down -> Right
3. Down -> Right -> Down

Constraints:

• 1 <= m, n <= 100

state transition equation:

initialization: F(0, 0) = 1

终止状态: F(m,n)

state transition equation: F(r, c) = F(r-1, c) + F(r, c-1)

509. Fibonacci Number

The Fibonacci numbers, commonly denoted F(n) form a sequence, called the Fibonacci sequence, such that each number is the sum of the two preceding ones, starting from 0 and 1. That is,

F(0) = 0, F(1) = 1
F(n) = F(n - 1) + F(n - 2), for n > 1.

Given n, calculate F(n).

Example 1:

Input: n = 2
Output: 1
Explanation: F(2) = F(1) + F(0) = 1 + 0 = 1.

Example 2:

Input: n = 3
Output: 2
Explanation: F(3) = F(2) + F(1) = 1 + 1 = 2.

Example 3:

Input: n = 4
Output: 3
Explanation: F(4) = F(3) + F(2) = 2 + 1 = 3.

Constraints:

• 0 <= n <= 30

Initialization:

n = 0, F(n) = 0

n = 1, F(n) = 1

F(n) = F(n - 1) + F(n - 2)

509

62

121

70

279

221

Reference

https://www.bilibili.com/video/BV1bX4y1M7WZ/?spm_id_from=333.999.0.0&vd_source=73e7d2c4251a7c9000b22d21b70f5635

https://www.bilibili.com/video/BV1Xj411K7oF/?spm_id_from=333.999.0.0&vd_source=73e7d2c4251a7c9000b22d21b70f5635

1. 自上而下的递归+备忘录
2. 自下而上的迭代 (动态规划问题的最优实现)

递归需要额外的栈空间

递归的层数存在局限性

根据他人经验 100 题 dp 题后才算入门

Google 最后的 coding 面试了 还在抱佛脚!!! (抱!!!) 希望面试官出简单的呜呜呜呜

1DP Summary:

1. dp[i] 物理意义, result 是怎样的

2. dp[0], dp[1] base case

3. dp[3] = ?, 寻找与 dp[0], dp[1] 之间的关系 寻找 induction rule

induction rule 比较难找的时候可以先将 dp 像表格一样填完, 规律可能会更好感受出来

4. dp[4] 用来验证 induction rule

5. write code

70. Climbing Stairs 作为例子进行按照上述总结进行求解

You are climbing a staircase. It takes n steps to reach the top.

Each time you can either climb 1 or 2 steps. In how many distinct ways can you climb to the top?

Example 1:

Input: n = 2
Output: 2
Explanation: There are two ways to climb to the top.
1. 1 step + 1 step
2. 2 steps

Example 2:

Input: n = 3
Output: 3
Explanation: There are three ways to climb to the top.
1. 1 step + 1 step + 1 step
2. 1 step + 2 steps
3. 2 steps + 1 step

Constraints:

• 1 <= n <= 45

Solution:

Step1:

一般题目求啥, 啥就是 dp[i]的物理意义

3                                                        ______
2                                      ___3___|
1                        __2____|
0       ___1___ |
     |
...

"In how many distinct ways can you climb to the top?"

-> dp[i]: means how many distinct ways you can climb to the i.

-> result = dp[n - i] 这个就是答案.

Step2:

物理意义设立出来之后, 开始寻找规律 -> 从最基础的开始

"Each time you can either climb 1 or 2 steps."

-> base case:

dp[0] = 1;

dp[1] = 2;

Step3:

dp[2] = ? -> 个人感觉 dp 最难的部分就是寻找 dp rule 的这个部分 (有的时候可以理解为填表)

先得出跳上第三个台阶的时候, 可以是 stair0 + starir(1,2) ; stair0 + stair1 + stair2; stair(0, 1) + stair2

共有三种方法 所以 dp[2] = 3;

dp[2] = dp[1] + dp[0] (似乎是对的) dp[i] = dp[i - 1] + dp[i - 2];

Step4:

用 dp[3] 求证

-1

/ \

0 [01]

/ \ / \

0,1 0,[12] [01],2 [01],[23]

/ \ | |

0,1,2 0,1,[23] 0,[12],3 [01],2,3

/

0,1,2,3

到达 stair 4 有 5 种方式

dp[3] = dp[2] + dp[1] = 3 + 2 = 5 (此处基本上满足验证了) 基本上就没有什么问题了.

-> dp[i] = dp[i-1] + dp[i-2]

dp[0] = 1;

dp[1] = 2;

这似乎很像高中里的数学里的数学归纳法(Mathematical Induction), 也像运筹学里的动态规划(但之前学的解法会有点儿不一样), 和计算机中的又像又不像, 总觉熟悉, 目前处于稍微混乱的感受. 熟悉又陌生. 感觉像是从不同角度阐述同一个东西.

证明：对任意正整数 \( n \)，有： $ 1 + 2 + 3 + \dots + n = \frac{n(n+1)}{2} $

解： 利用数学归纳法证明。

1. 基础步骤：当 \(n = 1\) 时，左边 $1 = \frac{1(1+1)}{2} = 1 $​，显然成立。

2. 归纳假设：假设当 $ n = k $ 时，等式成立，即： $1 + 2 + \dots + k = \frac{k(k+1)}{2} $

3. 归纳步骤：需要证明当 $n = k+1 $ 时，等式也成立。

即 $1 + 2 + \dots + k + (k+1) = \frac{(k+1)(k+2)}{2} $

左边： $1 + 2 + \dots + k + (k+1) = \frac{k(k+1)}{2} + (k+1) = \frac{k(k+1) + 2(k+1)}{2} = \frac{(k+1)(k+2)}{2} $

因此，当 $n = k+1 $ 时，等式成立。归纳法证明完毕。

-> 假设我的理解就是先找个规律

Step5:

class Solution {
    public int climbStairs(int n) {
        /*

        dp[i] means how many step to current i staircase
2                _
1           _
0        _
                 2 + 1
            1+1
dp[i]    1


        */
        if (n == 1){
            return 1;
        }
        int[] dp = new int[n];

        dp[0] = 1;
        dp[1] = 2;
        for (int i = 2; i < n; i++){
            dp[i] = dp[i - 1] + dp[i - 2];
        }

        return dp[n - 1];
    }
}

// TC: O(n)
// SC: O(n)

139. Word Break

Given a string s and a dictionary of strings wordDict, return true if s can be segmented into a space-separated sequence of one or more dictionary words.

Note that the same word in the dictionary may be reused multiple times in the segmentation.

Example 1:

Input: s = "leetcode", wordDict = ["leet","code"]
Output: true
Explanation: Return true because "leetcode" can be segmented as "leet code".

Example 2:

Input: s = "applepenapple", wordDict = ["apple","pen"]
Output: true
Explanation: Return true because "applepenapple" can be segmented as "apple pen apple".
Note that you are allowed to reuse a dictionary word.

Example 3:

Input: s = "catsandog", wordDict = ["cats","dog","sand","and","cat"]
Output: false

Constraints:

• 1 <= s.length <= 300
• 1 <= wordDict.length <= 1000
• 1 <= wordDict[i].length <= 20
• s and wordDict[i] consist of only lowercase English letters.
• All the strings of wordDict are unique.

Solution:

Step1: dp[i] mean

" return true if s can be segmented into a space-separated sequence of one or more dictionary words."

dp[i] means: whether true i can segment word from 0 to i and in the dirctionary

Step2: dp[i] base case

dp[0] = True

198. House Robber

You are a professional robber planning to rob houses along a street. Each house has a certain amount of money stashed, the only constraint stopping you from robbing each of them is that adjacent houses have security systems connected and it will automatically contact the police if two adjacent houses were broken into on the same night.

Given an integer array nums representing the amount of money of each house, return *the maximum amount of money you can rob tonight without alerting the police*.

Example 1:

Input: nums = [1,2,3,1]
Output: 4
Explanation: Rob house 1 (money = 1) and then rob house 3 (money = 3).
Total amount you can rob = 1 + 3 = 4.

Example 2:

Input: nums = [2,7,9,3,1]
Output: 12
Explanation: Rob house 1 (money = 2), rob house 3 (money = 9) and rob house 5 (money = 1).
Total amount you can rob = 2 + 9 + 1 = 12.

Constraints:

• 1 <= nums.length <= 100
• 0 <= nums[i] <= 400

322. Coin Change

You are given an integer array coins representing coins of different denominations and an integer amount representing a total amount of money.

Return the fewest number of coins that you need to make up that amount. If that amount of money cannot be made up by any combination of the coins, return -1.

You may assume that you have an infinite number of each kind of coin.

Example 1:

Input: coins = [1,2,5], amount = 11
Output: 3
Explanation: 11 = 5 + 5 + 1

Example 2:

Input: coins = [2], amount = 3
Output: -1

Example 3:

Input: coins = [1], amount = 0
Output: 0

Constraints:

• 1 <= coins.length <= 12
• 1 <= coins[i] <= 231 - 1
• 0 <= amount <= 104

300. Longest Increasing Subsequence

• 1 <= nums.length <= 2500
• -104 <= nums[i] <= 104

Follow up: Can you come up with an algorithm that runs in O(n log(n)) time complexity?

2D Summary

5. Longest Palindromic Substring

72. Edit Distance

1130. Minimum Cost Tree From Leaf Values

Knapsack

0-1 Knapsack

0-1 背包: 有\(n\) 个物品, 第\(i\) 个物品的体积为\(w[i]\), 价值为\(v[i]\), 每个物品至多选一个, 求体积和不超过 capacity 时的最大价值和

回溯三问:

1. 当前操作? 枚举第\(i\) 个物品选或不选:

不选, 剩余容量不变; 选, 剩余容量减少\(w[i]\)

2. 子问题? 在剩余容量为 c 时, 从前\(i\) 个物品中得到的最大价值和

3. 下一个子问题? 分类讨论:

不选: 在剩余容量为\(c\) 时, 从前\(i - 1\) 个物品中得到的最大价值和

选: 在剩余容量为\(c - w[i]\) 时, 从前\(i - 1\)个物品中得到的最大价值和

\[ dfs(i, c) = max(dfs(i - 1, c), dfs(i - 1, c - w[i]) + v[i]) \]

494

回溯

记忆化搜索

递推

空间优化: 两个数组

空间优化: 一个数组

完全背包

322

常见变形

1. 至多装 capacity, 求方案数/最大价值和
2. 恰好装 capacity, 求方案数/最大/最小价值和
3. 至少装 capacity, 求方案数/最小价值和

\[ dfs(i, c) = dfs(i - 1, c)+ dfs(i - 1, c - w[i]) \]

Linear DP

1143

72

转移优化/证明

空间优化: 一个数组

子数组/子串 subarray/substring

子序列 subsequence

State Machine DP

不限交易次数

122

309

714

至多交易 k 次

188

121 (k = 1)

123 (k = 2)

Interval DP

区间 dp:

1. 区别:

线性 DP: 一般是在前缀/后缀上转移

区间 DP: 从小区间转移到大区间

2. 选或不选:

从两侧向内缩小问题规模

516

3. 枚举选哪个

分割成多个规模更小的子问题

1039

Tree DP

Tree Diameter

二叉树

104

思考整棵树与其左右子树的关系

愿问题: 整棵树

子问题: 左子树, 右子树

整棵树的最大深度 = max(左子树的最大深度, 右子树的最大深度)

直径和最大深度, 是否有联系呢?

边权型 543

点权型 124

一般树

一般树的性质

1245

2246

House Robber III

Binary Tree Cameras

运筹学

动态规划 运筹学中也提及过 或许从计算机角度和数学角度 虽然在探讨一个问题, 但是不同的角度, 也许是因为理解不到位, 总是碰撞.

一维资源分配问题:可以被看作是一种 01 背包问题