Backtracking

• 子集型
• 组合型
• 排列型

Subsets

1. 多重循环到回溯 17. Letter Combinations of a Phone Number

2. 回溯三问: 思考回溯问题的套路

3. 子集型回溯

3.1 lc 78

3.2 lc 131

4. 两种思路

4.1 输入的视角

4.2 答案的视角

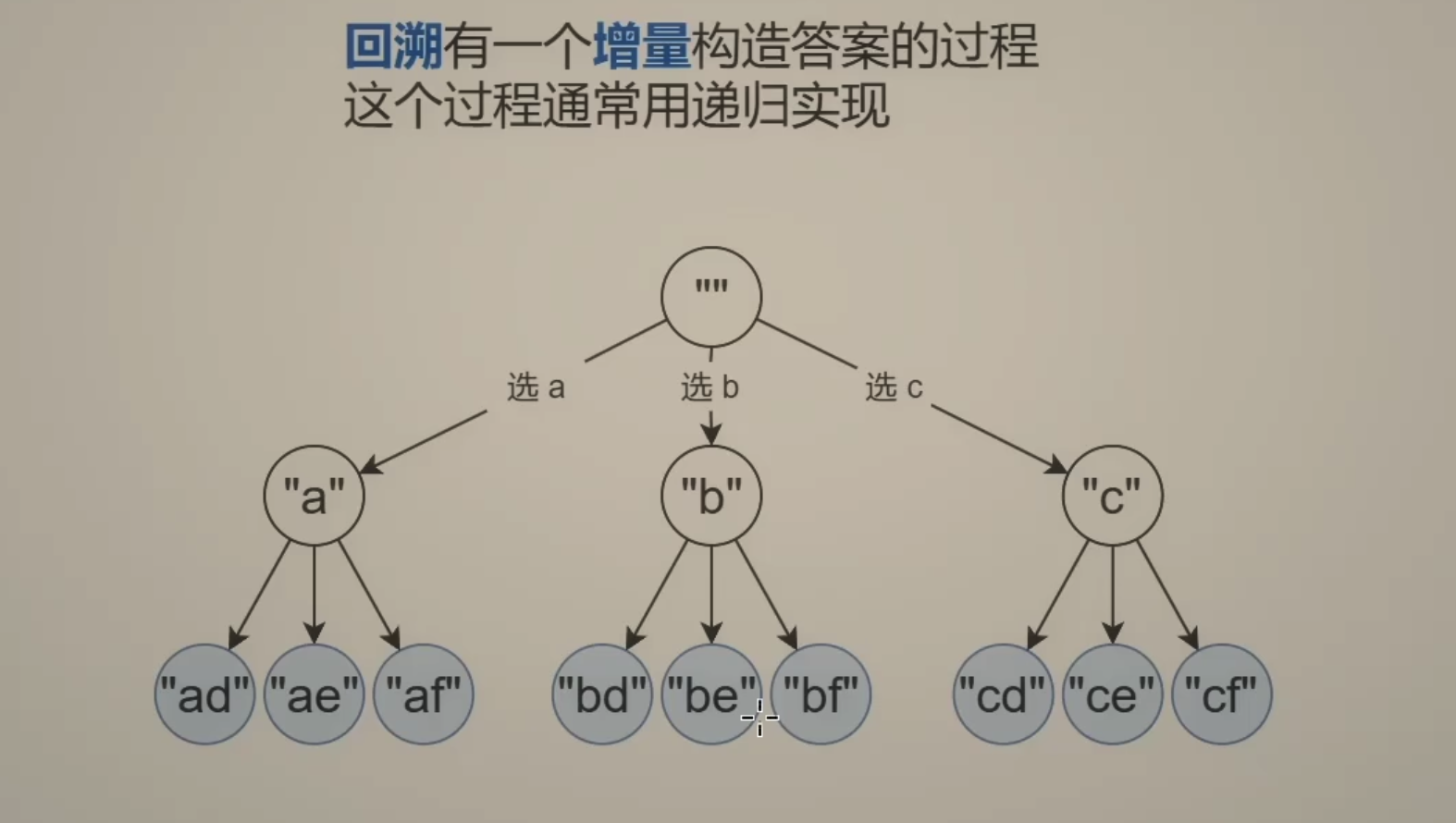
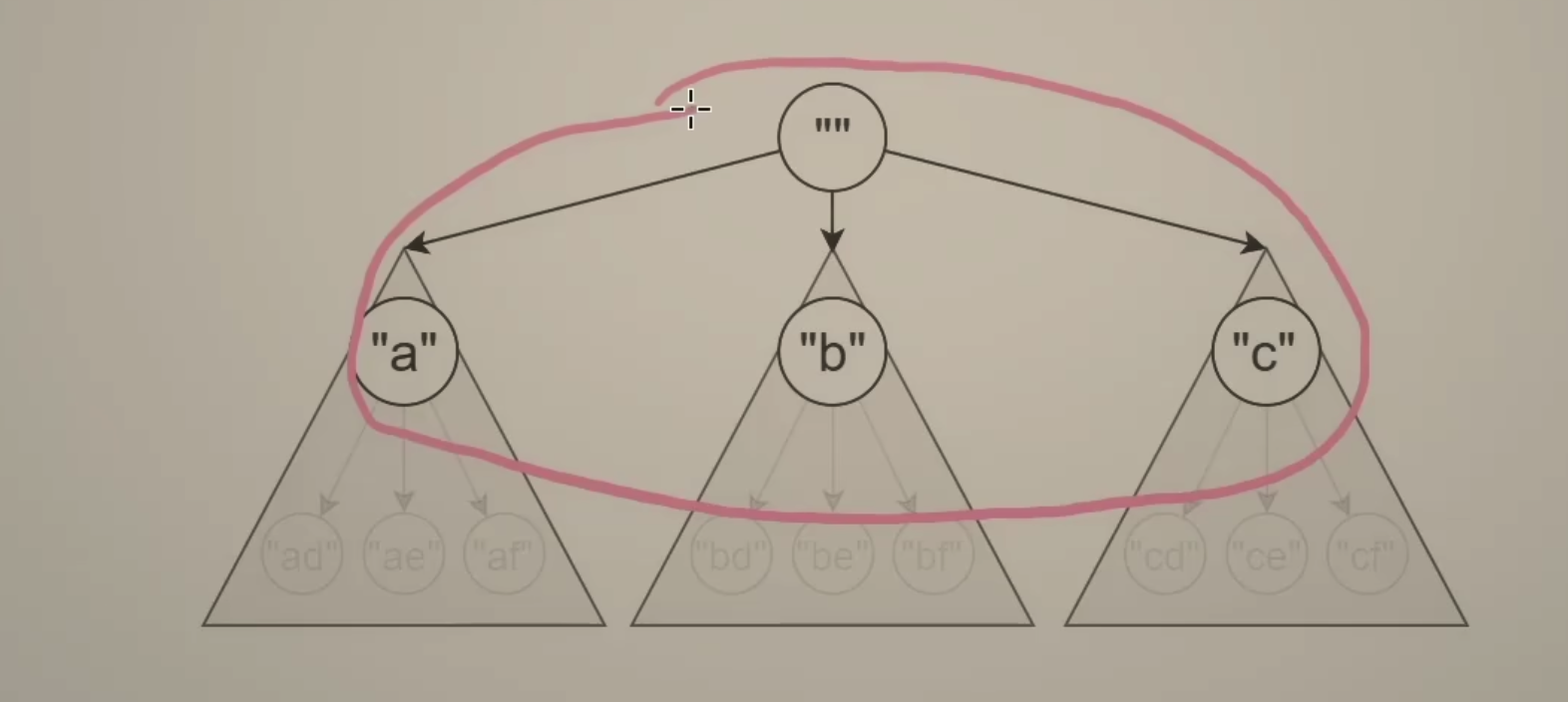
用一个path数组记录路径上的字母

回溯三问:

1. 当前操作? 枚举path[i] 要填入的字母
2. 子问题? 构造字符串\(\geq i\) 的部分
3. 下一个子问题? 构造字符串\(\geq i + 1\) 的部分

\(dfs(i) \rightarrow dfs(i + 1)\)

子集型回溯

每个元素都可以选/不选

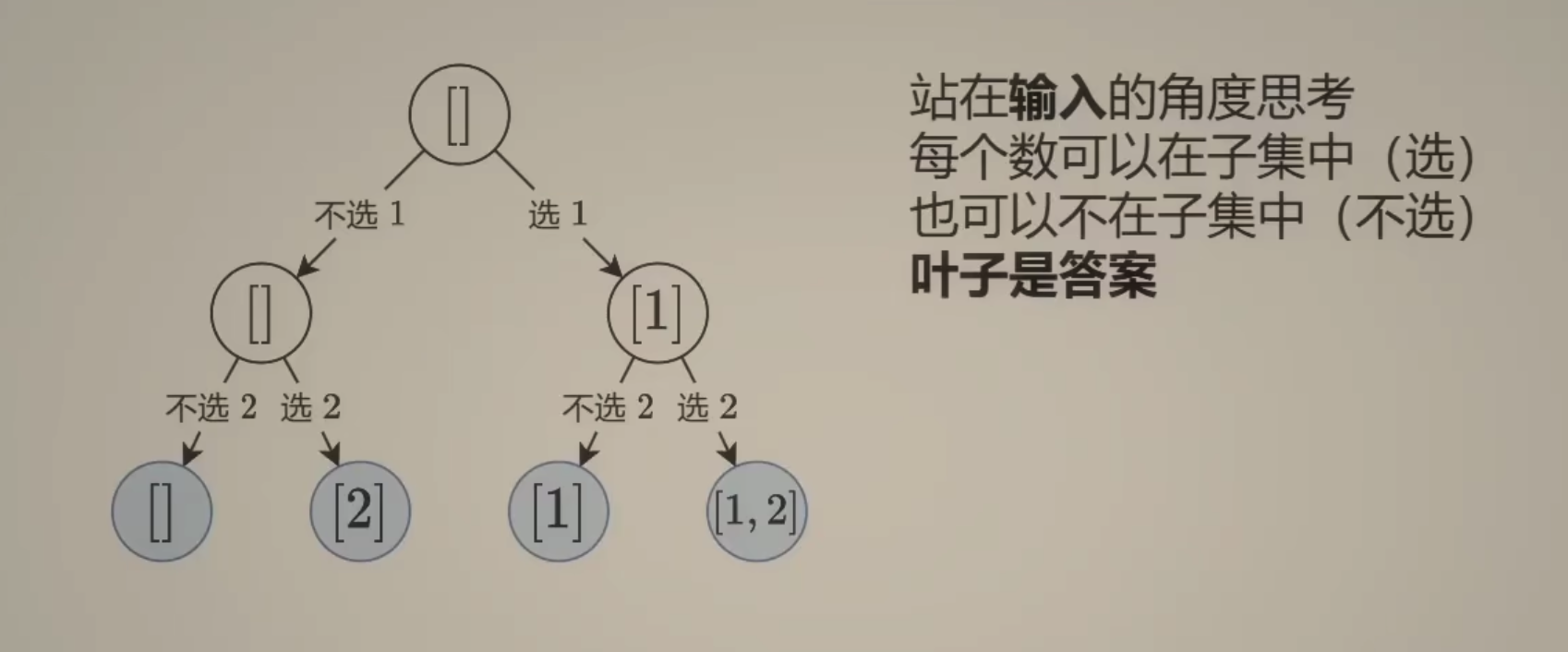
回溯三问:

1. 当前操作? 枚举第i个数选/不选 (branch meaing)
2. 子问题? 从下标\(\ge i\) 的数字中构造子集
3. 下一个子问题? 从下标\(\geq i + 1\) 的数字中构造子集

\(dfs(i) \rightarrow dfs(i + 1)\)

1. Define branch, level meaning
2. Draw tree

public int backtrack(STATE curr, OTHER_ARGUMENTS...){
  if (BASE_CASE){
    return 0;
  }

  int ans = 0;

  for (ITERATE_OVER_INPUT){
    ans += backtrack(curr, OTHER_ARGUEMNTS...)
  }
}

Backtracking vs DFS

Backtracking is a more general purpose algorithm.

DFS is a specific form of backtracking related to searching tree structures.

From Wikipedia:

One starts at the root (selecting some node as the root in the graph case) and explores as far as possible along each branch before backtracking.

It uses backtracking as part of its means of working with a tree, but is limited to a tree structure.

Backtracking, though, can be used on any type of structure where portions of the domain can be eliminated - whether or not it is a logical tree. The Wiki example uses a chessboard and a specific problem - you can look at a specific move, and eliminate it, then backtrack to the next possible move, eliminate it, etc.

https://stackoverflow.com/questions/1294720/whats-the-difference-between-backtracking-and-depth-first-search

39. Combination Sum

Given an array of distinct integers candidates and a target integer target, return a list of all unique combinations of candidates where the chosen numbers sum to target. You may return the combinations in any order.

The same number may be chosen from candidates an unlimited number of times. Two combinations are unique if the frequency of at least one of the chosen numbers is different.

The test cases are generated such that the number of unique combinations that sum up to target is less than 150 combinations for the given input.

Example 1:

Input: candidates = [2,3,6,7], target = 7
Output: [[2,2,3],[7]]
Explanation:
2 and 3 are candidates, and 2 + 2 + 3 = 7. Note that 2 can be used multiple times.
7 is a candidate, and 7 = 7.
These are the only two combinations.

Example 2:

Input: candidates = [2,3,5], target = 8
Output: [[2,2,2,2],[2,3,3],[3,5]]

Example 3:

Input: candidates = [2], target = 1
Output: []

Solution:

Define

branch: how many take current candidates[i]

level: candidates[i]

class Solution {
    public List<List<Integer>> combinationSum(int[] candidates, int target) {
        List<List<Integer>> result = new ArrayList<>();

        List<Integer> subResult = new ArrayList<Integer>();

        int curSum = 0;
        int index = 0;
        backtracking(index, target, candidates, curSum, subResult, result);
        return result;

    }

    private void backtracking(int index, int target, int[] candidates, int curSum, List<Integer> subResult, List<List<Integer>> result){
        // base case
        if (index == candidates.length){
            if (curSum == target){
                result.add(new ArrayList<Integer>(subResult));
                return;
            }
            return;
        }

        if (curSum > target){
            return;
        }

        int cur = candidates[index];

        // branch
        int maxTake = (target - curSum) / cur;
        for (int i = 0; i <= maxTake; i++){
            for(int j = 0; j < i; j++){
                subResult.add(cur);
            }
            backtracking(index + 1, target, candidates, curSum + cur * i, subResult, result);
            for (int k = 0; k < i; k++){
                subResult.remove(subResult.size() - 1);
            }

        }
    }
}
// k = candidates.length
// level = Math.max(target/Math.min(candidates[i]))
// TC: O(branch^level) = O(k^n)
// SC: O(target/Math.min(candidates[i]))

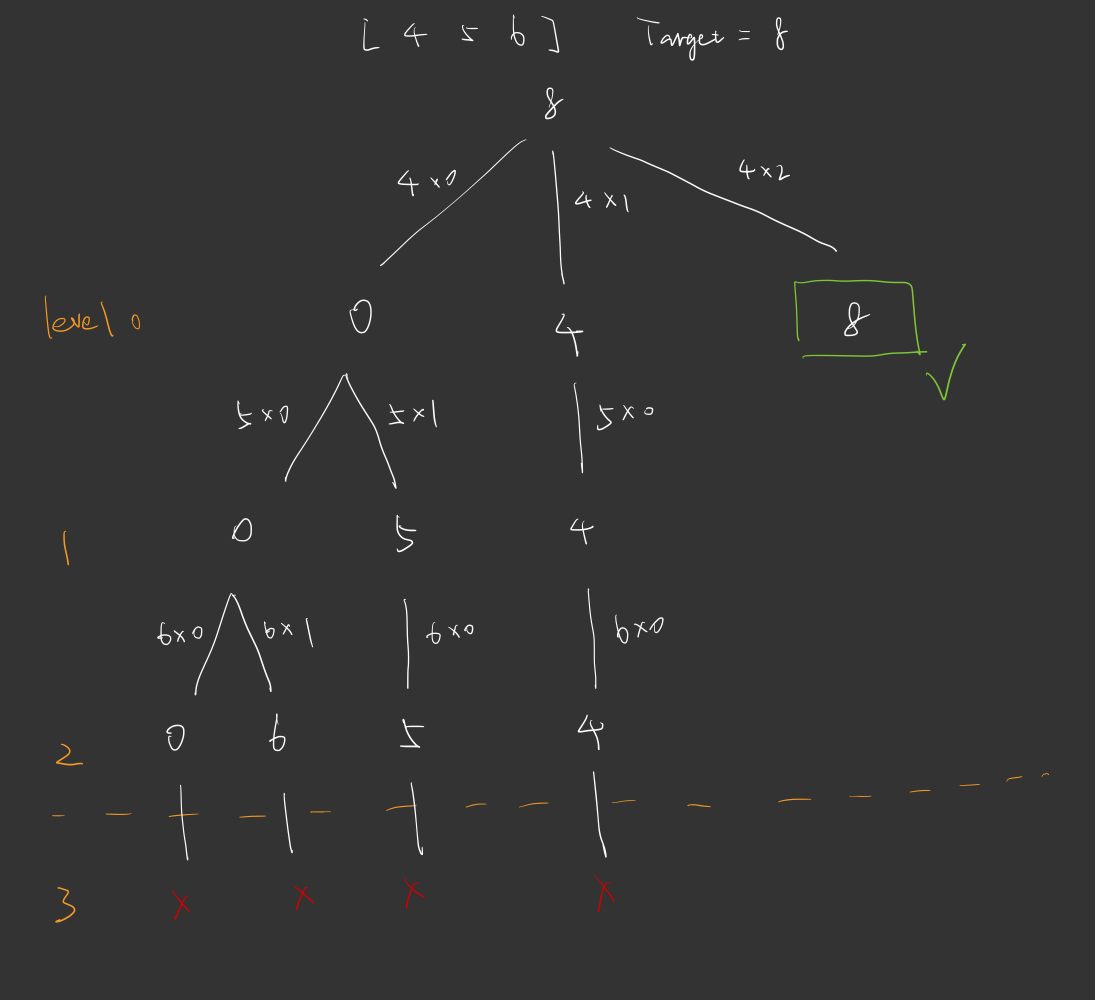
很重要呀很重要呀!

• 39. Combination Sum
• 40. Combination Sum II
• 216. Combination Sum III
• 377. Combination Sum IV
• 22. Generate Parentheses
• 46. Permutations
• 47. Permutations II
• 77. Combinations
• 78. Subsets
• 90. Subsets II
• 51. N-Queens
• 36. Valid Sudoku
• 131. Palindrome Partitioning
• 132. Palindrome Partitioning II
• 1278. Palindrome Partitioning III
• 1745. Palindrome Partitioning IV

Combinations

77

216

22

301

39

Permutations

46

51

357

2850