Trie
1 What is Trie?
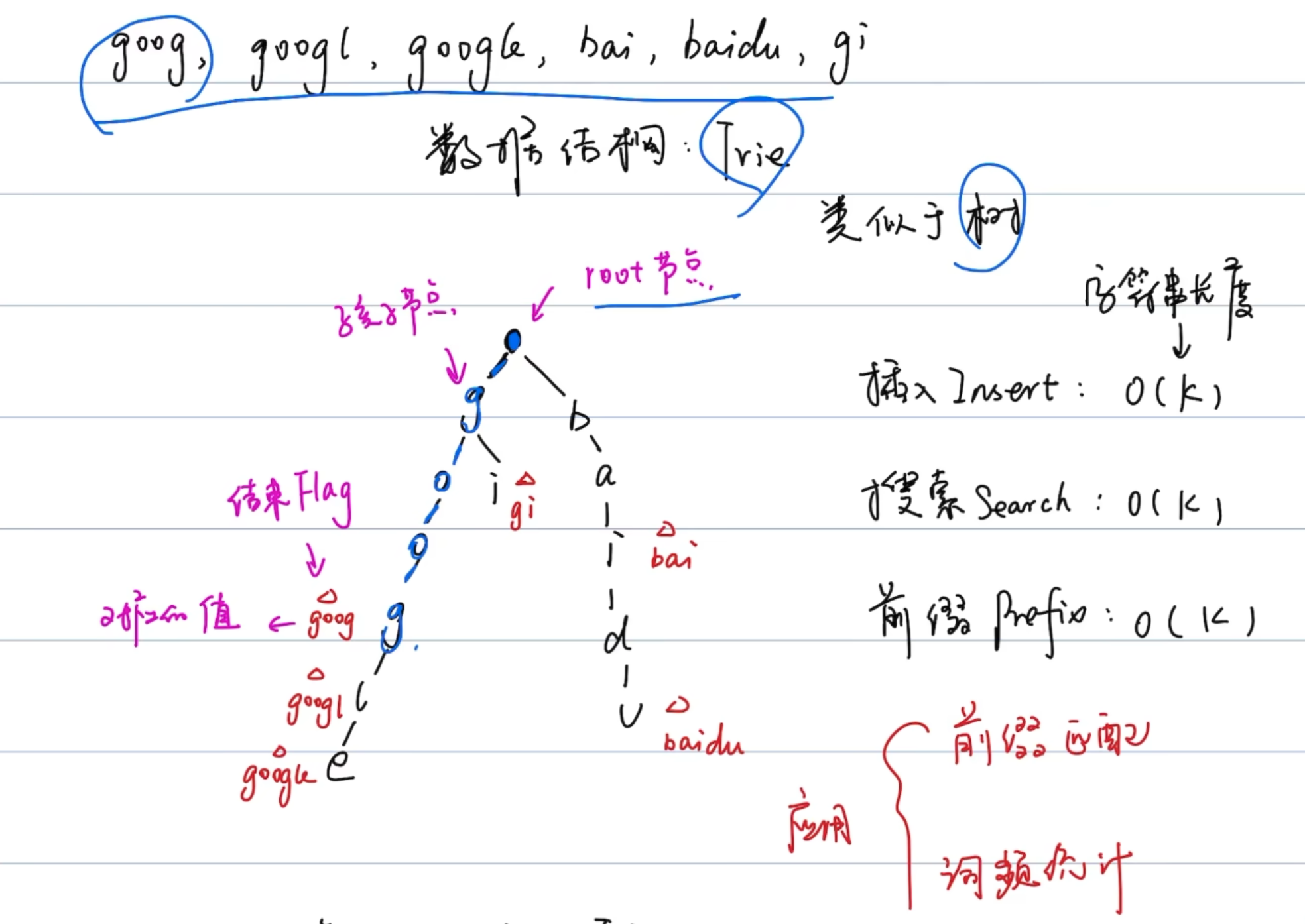
A Trie is a special form of a Nary tree. Typically, a trie is used to store strings. Each Trie node represents a string (a prefix). Each node might have several children nodes while the paths to different children nodes represent different characters. And the strings the child nodes represent will be the origin string represented by the node itself plus the character on the path.
Here is an example of a trie:

In the example, the value we mark in each node is the string the node represents. For instance, we start from the root node and choose the second path 'b', then choose the first child 'a', and choose child 'd', finally we arrived at the node "bad". The value of the node is exactly formed by the letters in the path from the root to the node sequentially.
It is worth noting that the root node is associated with the empty string.
One important property of Trie is that all the descendants of a node have a common prefix of the string associated with that node. That's why Trie is also called prefix tree.
Let's look at the example again. For example, the strings represented by nodes in the subtree rooted at node "b" have a common prefix "b". And vice versa. The strings which have the common prefix "b" are all in the subtree rooted at node "b" while the strings with different prefixes will come to different branches.
Trie is widely used in various applications, such as autocomplete, spell checker, etc.
2 How to represent a Trie?
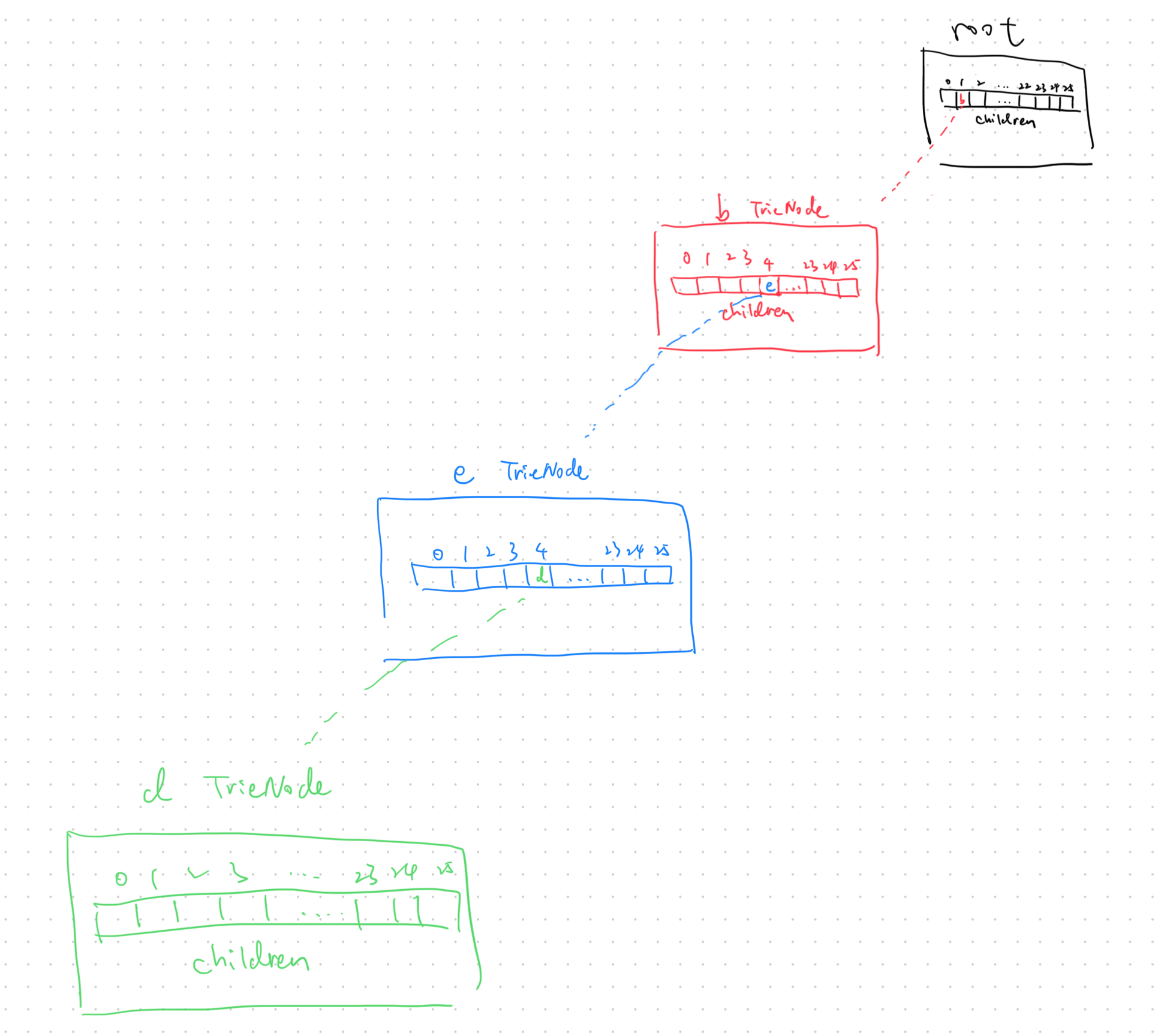
What's special about Trie is the corresponding relationship between characters and children nodes. There are a lot of different representations of a trie node. Here we provide two of them.
2.1 Array
The first solution is to use an array to store children nodes.
For instance, if we store strings which only contains letter a to z, we can declare an array whose size is 26 in each node to store its children nodes. And for a specific character c, we can use c - 'a' as the index to find the corresponding child node in the array.
class Trie {
class TrieNode{
TrieNode[] children = new TrieNode[26];
}
TrieNode root;
public Trie() {
root = new TrieNode();
}
}
It is really fast to visit a child node. It is comparatively easy to visit a specific child since we can easily transfer a character to an index in most cases. But not all children nodes are needed. So there might be some waste of space.
2.2 Map
The second solution is to use a hashmap to store children nodes.
We can declare a hashmap in each node. The key of the hashmap are characters and the value is the corresponding child node.
class Trie {
class TrieNode{
Map<Character, TrieNode> children = new HashMap<>();
}
TrieNode root;
public Trie() {
root = new TrieNode();
}
}
It is even easier to visit a specific child directly by the corresponding character. But it might be a little slower than using an array. However, it saves some space since we only store the children nodes we need. It is also more flexible because we are not limited by a fixed length and fixed range.
2.3 More
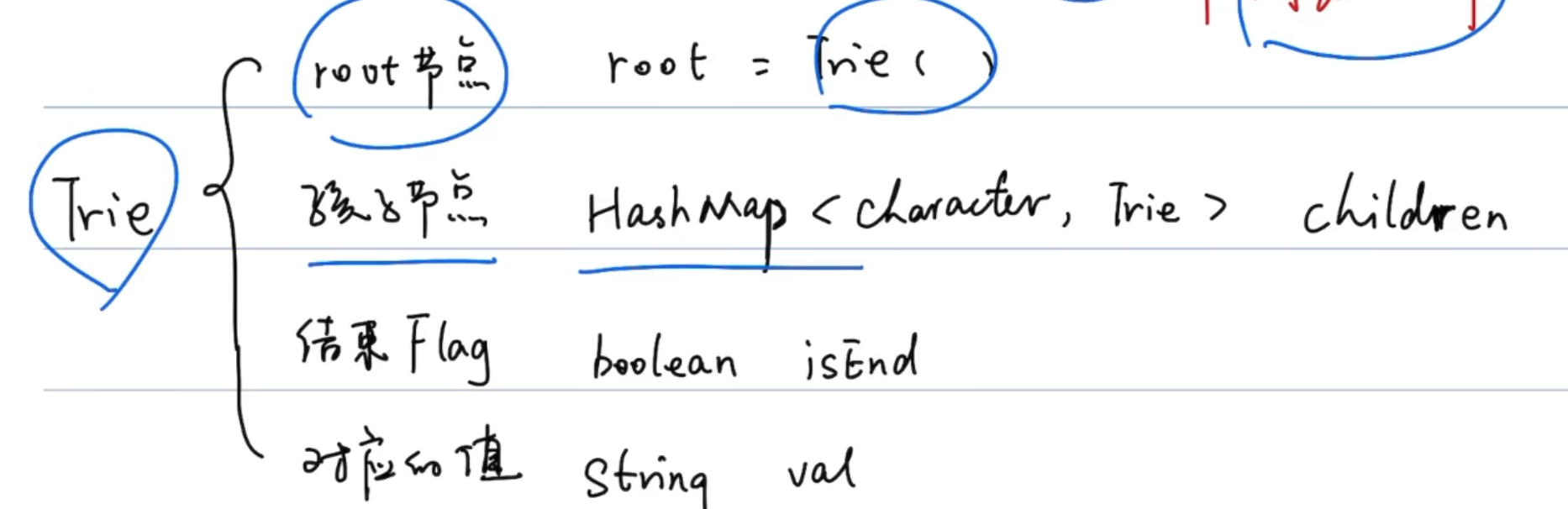
We mentioned how to represent the children nodes in Trie node. Besides, we might need some other values.
For example, as we know, each Trie node represents a string but not all the strings represented by Trie nodes are meaningful. If we only want to store words in a Trie, we might declare a boolean in each node as a flag to indicate if the string represented by this node is a word or not.
3 Basic Operations
3.1 Insertion in Trie
class Trie {
class TrieNode{
TrieNode[] children = new TrieNode[26];
}
TrieNode root;
public Trie() {
root = new TrieNode();
}
public void insert(String word) {
TrieNode cur = root;
for (int i = 0; i < word.length(); i++){
TrieNode next = cur.children[word.charAt(i) - 'a'];
if (next == null){
next = new TrieNode();
cur.children[word.charAt(i) - 'a'] = next;
}
cur = next;
}
}
}
eg. insert bed
3.2 Search in Trie
3.2.1 Search Prefix
As we mentioned in the introduction to Trie, all the descendants of a node have a common prefix of the string associated with that node. Therefore, it should be easy to search if there are any words in the trie that starts with the given prefix.
Similarly, we can go down the tree depending on the given prefix. Once we can not find the child node we want, search fails. Otherwise, search succeeds.
class Trie {
class TrieNode{
TrieNode[] children = new TrieNode[26];
boolean isWord = false;
}
TrieNode root;
public Trie() {
root = new TrieNode();
}
public void insert(String word) {
TrieNode cur = root;
for (int i = 0; i < word.length(); i++){
TrieNode next = cur.children[word.charAt(i) - 'a'];
if (next == null){
next = new TrieNode();
cur.children[word.charAt(i) - 'a'] = next;
}
cur = next;
}
cur.isWord = true;
}
public boolean searchPrefix(String prefix) {
TrieNode cur = root;
for (int i = 0; i < prefix.length(); i++){
TrieNode next = cur.children[prefix.charAt(i) - 'a'];
if (next == null){
return false;
}
cur = next;
}
return true;
}
}
3.2.2 Search Word
You might also want to know how to search for a specific word rather than a prefix. We can treat this word as a prefix and search in the same way we mentioned above.
- If search fails which means that no words start with the target word, the target word is definitely not in the Trie.
- If search succeeds, we need to check if the target word is only a prefix of words in Trie or it is exactly a word. To solve this problem, you might want to modify the node structure a little bit.
Hint: A boolean flag in each node might work.
class Trie {
class TrieNode{
TrieNode[] children = new TrieNode[26];
boolean isWord = false;
}
TrieNode root;
public Trie() {
root = new TrieNode();
}
public void insert(String word) {
TrieNode cur = root;
for (int i = 0; i < word.length(); i++){
TrieNode next = cur.children[word.charAt(i) - 'a'];
if (next == null){
next = new TrieNode();
cur.children[word.charAt(i) - 'a'] = next;
}
cur = next;
}
cur.isWord = true;
}
public boolean search(String word) {
TrieNode cur = root;
for (int i = 0; i < word.length(); i++){
TrieNode next = cur.children[word.charAt(i) - 'a'];
if (next == null){
return false;
}
cur = next;
}
if (cur.isWord == true){
return true;
}else {
return false;
}
}
}
4 Template
208. Implement Trie (Prefix Tree)
package data_structures.trie;
import java.util.HashMap;
import java.util.Map;
public class Trie {
private final TrieNode root;
private static class TrieNode{
Map<Character, TrieNode> children = new HashMap<>();
boolean isWord;
}
// TrieNode 本身是一个通用节点结构,只存储子节点和是否为单词结尾的信息。它的行为完全独立于 Trie 的实例
// 如果 TrieNode 是非 static 的,节点与 Trie 的实例会产生隐式的耦合
public Trie(){
root = new TrieNode();
}
public void insert(String word){ // L = word.length
TrieNode cur = root;
for (int i = 0; i < word.length(); i++){
char ch = word.charAt(i);
if (!cur.children.containsKey(ch)) {
cur.children.put(ch, new TrieNode());
}
cur = cur.children.get(ch);
}
cur.isWord = true;
}
// TC: O(L)
public boolean search(String word){
TrieNode cur = root;
for (int i = 0; i < word.length(); i++){
char ch = word.charAt(i);
if (!cur.children.containsKey(ch)){
return false;
}else{
cur = cur.children.get(ch);
}
}
return cur.isWord;
}
// TC: O(L)
public boolean startsWith(String prefix){
TrieNode cur = root;
for (int i = 0; i < prefix.length(); i++){
char ch = prefix.charAt(i);
if (cur.children.containsKey(ch)){
cur = cur.children.get(ch);
}else{
return false;
}
}
return true;
}
// TC: O(P)
}
// n words
// TC: O(L)
// SC: O(N*L)
5 Practical Application I
Trie is widely used to store strings and retrieve keywords, especially prefix related keywords.
The practical application scenarios of Trie can be very straightforward. Typically, you will need to provide insert method and some kind of search operation related to prefix of words. We provide exercises for you to practice in this chapter.

One simple way to implement autocomplete is to store ngrams in Trie and do recommendation based on frequency. Consider thoroughly that what will be an ideal node structure to solve this problem.
It is easy to find words with same prefix in Trie. But how about finding similar words instead? You might want to use some search algorithm to solve this problem.
211. Design Add and Search Words Data Structure
class WordDictionary {
static class Trie{
static class TrieNode{
Map<Character, TrieNode> children = new HashMap<>();
boolean isWord = false;
}
TrieNode root;
public Trie(){
root = new TrieNode();
}
public void insert(String word) {
TrieNode cur = root;
for (char ch : word.toCharArray()){
if (cur.children.containsKey(ch)){
cur = cur.children.get(ch);
}else{
cur.children.put(ch, new TrieNode());
cur = cur.children.get(ch);
}
}
cur.isWord = true;
}
public boolean search(String word){
TrieNode cur = root;
return search(word, cur);
}
public boolean search(String word, TrieNode cur) {
for (int i = 0; i < word.length(); i++){
char ch = word.charAt(i);
if (!cur.children.containsKey(ch)){
if (ch == '.'){
for (Map.Entry<Character, TrieNode> e : cur.children.entrySet()){
TrieNode child = e.getValue();
if (search(word.substring(i + 1), child) == true){
return true;
}
}
}
return false;
}else{
cur = cur.children.get(ch);
}
}
return cur.isWord;
}
}
Trie trie;
public WordDictionary() {
trie = new Trie();
}
public void addWord(String word) {
trie.insert(word);
}
public boolean search(String word) {
return trie.search(word);
}
}
/**
* Your WordDictionary object will be instantiated and called as such:
* WordDictionary obj = new WordDictionary();
* obj.addWord(word);
* boolean param_2 = obj.search(word);
*/
class MapSum {
static Map<String, Integer> map;
Trie trie;
public MapSum() {
map = new HashMap<>();
trie = new Trie();
}
class Trie{
static class TrieNode{
Map<Character, TrieNode> children = new HashMap<>();
int score = 0;
}
private TrieNode root;
public Trie(){
root = new TrieNode();
}
public void insert(String key, int val) {
TrieNode cur = root;
int delta = val - map.getOrDefault(key, 0);
map.put(key, val);
cur.score = cur.score + delta;
for (char c : key.toCharArray()){
cur.children.putIfAbsent(c, new TrieNode());
cur = cur.children.get(c);
cur.score += delta;
}
}
public int sum(String prefix) {
TrieNode cur = root;
for (char c : prefix.toCharArray()){
cur = cur.children.get(c);
if (cur == null){
return 0;
}
}
return cur.score;
}
}
public void insert(String key, int val) {
trie.insert(key, val);
}
public int sum(String prefix) {
return trie.sum(prefix);
}
}
/**
* Your MapSum object will be instantiated and called as such:
* MapSum obj = new MapSum();
* obj.insert(key,val);
* int param_2 = obj.sum(prefix);
*/
642. Design Search Autocomplete System
class AutocompleteSystem {
static class TrieNode{
Map<Character, TrieNode> children = new HashMap<>();
Map<String, Integer> frequencyMap = new HashMap<>();
}
static class Trie{
TrieNode root;
Trie(){
root = new TrieNode();
}
public void insert(String sentence, int time){
TrieNode cur = root;
for (char c : sentence.toCharArray()){
cur.children.putIfAbsent(c, new TrieNode());
cur = cur.children.get(c);
cur.frequencyMap.put(sentence, cur.frequencyMap.getOrDefault(sentence, 0) + time);
}
}
public Map<String, Integer> search(String prefix){
TrieNode cur = root;
for (char c : prefix.toCharArray()){
if (!cur.children.containsKey(c)){
return new HashMap<>();
}
cur = cur.children.get(c);
}
return cur.frequencyMap;
}
}
private final Trie trie;
private final StringBuilder currentInput;
public AutocompleteSystem(String[] sentences, int[] times) {
trie = new Trie();
currentInput = new StringBuilder();
for (int i = 0; i < sentences.length; i++){
trie.insert(sentences[i], times[i]);
}
}
public List<String> input(char c){
if (c == '#'){
String sentence = currentInput.toString();
trie.insert(sentence, 1);
currentInput.setLength(0);
return new ArrayList<>();
}
currentInput.append(c);
String prefix = currentInput.toString();
Map<String, Integer> frequencyMap = trie.search(prefix);
// PriorityQueue<String> pq = new PriorityQueue<>((a, b) -> (frequencyMap.get(b) - frequencyMap.get(a)));// maxheap
// 优先队列比较器:按频率降序,频率相同时按字典序升序
PriorityQueue<String> pq = new PriorityQueue<>((a, b) -> {
int freqCompare = frequencyMap.get(b).compareTo(frequencyMap.get(a));
return freqCompare != 0 ? freqCompare : a.compareTo(b);
});
for (String sentence : frequencyMap.keySet()){
pq.offer(sentence);
}
List<String> result = new ArrayList<>();
for (int i = 0; i < 3 && !pq.isEmpty(); i++){
result.add(pq.poll());
}
return result;
}
}
/**
* Your AutocompleteSystem object will be instantiated and called as such:
* AutocompleteSystem obj = new AutocompleteSystem(sentences, times);
* List<String> param_1 = obj.input(c);
*/
6 Practical Application II
In the previous chapter, we practice with some typical Trie problems. However, the practical applications of Trie are not always so straightforward.
In this chapter, we provide some interesting practical applications for you to get to know more possibilities about Trie
- Accelerate DFS
Sometimes, we will use Trie to accelerate DFS especially when we do DFS for word games. We provide two word games (Word Squares, Word Search II) for you in this chapter. Try to solve the problem by DFS first and then use Trie to improve the performance.
- Store other Data Type
We use Trie to store strings in most cases but not always. Maximum XOR of Two Numbers in an Array is an interesting example.
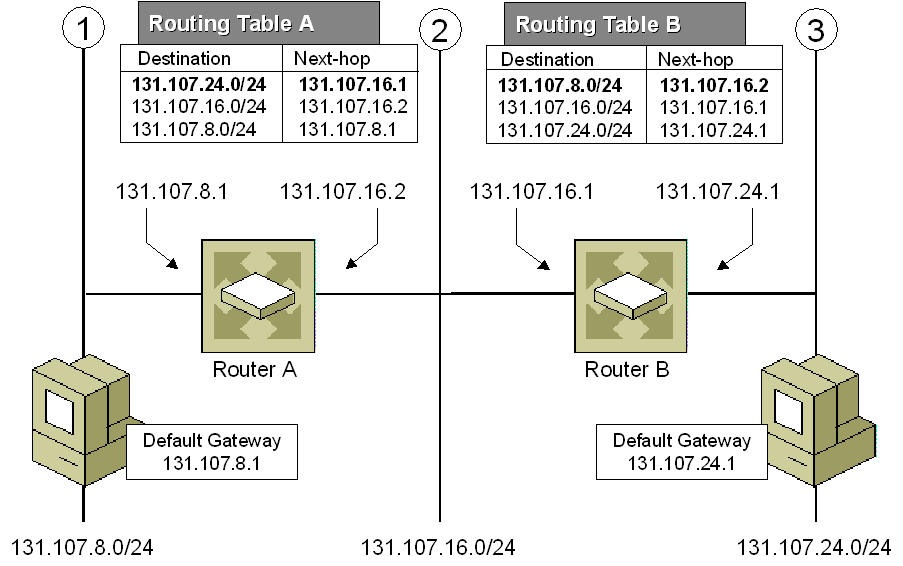
There are also some other use cases, such as IP routing (Longest prefix matching).
class Solution {
static class TrieNode{
Map<Character, TrieNode> children = new HashMap<>();
Boolean isWord = false;
}
static class Trie{
TrieNode root;
Trie(){
root = new TrieNode();
}
public void insert(String word){
TrieNode cur = root;
for (char c : word.toCharArray()){
cur.children.putIfAbsent(c, new TrieNode());
cur = cur.children.get(c);
}
cur.isWord = true;
}
}
public List<String> findWords(char[][] board, String[] words) {
List<String> result = new ArrayList<>();
Trie trie = new Trie();
for (String word : words){
trie.insert(word);
}
boolean[][] visited = new boolean[board.length][board[0].length];
StringBuilder sb = new StringBuilder();
for (int i = 0; i < board.length; i++){
for (int j = 0; j < board[0].length; j++){
helper(board, i, j, trie.root, sb, result, visited);
}
}
return result;
}
private void helper(char[][] board, int x, int y, TrieNode node, StringBuilder sb, List<String> result, boolean[][] visited){
int rows = board.length;
int cols = board[0].length;
if (x < 0 || x >= rows || y < 0 || y >= cols || visited[x][y]){
return;
}
char ch = board[x][y];
if (!node.children.containsKey(ch)){
return;
}
sb.append(ch);
node = node.children.get(ch);
if (node.isWord == true){
result.add(sb.toString());
node.isWord = false; // // 防止重复加入相同单词
}
visited[x][y] = true;
// four directions
helper(board, x + 1, y, node, sb, result, visited);
helper(board, x - 1, y, node, sb, result, visited);
helper(board, x, y + 1, node, sb, result, visited);
helper(board, x, y - 1, node, sb, result, visited);
visited[x][y] = false;
sb.deleteCharAt(sb.length() - 1);
}
}
class Solution {
static class TrieNode{
Map<Character, TrieNode> children = new HashMap<>();// 26
List<String> wordsWithPrefix = new ArrayList<String>(); // n
Boolean isWord = false;
}
static class Trie{
static TrieNode root;
Trie(){
root = new TrieNode();
}
// insert
public static void insert(String word){
TrieNode cur = root;
for (char c : word.toCharArray()){ // 26 * n * L
cur.children.putIfAbsent(c, new TrieNode());
cur.wordsWithPrefix.add(word);
cur = cur.children.get(c);
}
Boolean isWord = true;
}
// search
public static List<String> search(String prefix){
TrieNode cur = root;
for (char c : prefix.toCharArray()){
if (!cur.children.containsKey(c)){
return new ArrayList<>();
}
cur = cur.children.get(c);
}
return cur.wordsWithPrefix;
}
}
public List<List<String>> wordSquares(String[] words) {
List<List<String>> result = new ArrayList<>();
if (words == null || words.length == 0){
return result;
}
Trie trie = new Trie();
for (String word : words){
trie.insert(word);
}
List<String> subResult = new ArrayList<>();
for (String word : words){
subResult.add(word);
backtrack(1, subResult, trie, result);
subResult.remove(subResult.size() - 1);
}
return result;
}
private void backtrack(int step, List<String> subResult, Trie trie, List<List<String>> result){
if (step == subResult.get(0).length()){
result.add(new ArrayList<>(subResult));
return;
}
StringBuilder prefixBuilder = new StringBuilder();
for (String word : subResult){
prefixBuilder.append(word.charAt(step));
}
String prefix = prefixBuilder.toString();
List<String> find = trie.search(prefix);
for (String word : find){
subResult.add(word);
backtrack(step + 1, subResult, trie, result);
subResult.remove(subResult.size() - 1);
}
}
}
// TC: O(n * L * 26)
// SC: O(n*L)
/**
b a b a
i
a b a t
b a b a
a t a l
Problem List
6.1 Basics
- 208. Implement Trie (Prefix Tree)
- 211. Design Add and Search Words Data Structure
- 14. Longest Common Prefix
- 648. Replace Words
- 677. Map Sum Pairs
- 720. Longest Word in Dictionary
- 1268. Search Suggestions System
- 1233. Remove Sub-Folders from the Filesystem
- 820. Short Encoding of Words
- 2416. Sum of Prefix Scores of Strings
- 2261. K-Divisible Elements Subarrays
- 1804. Implement Trie II (Premium)
- 2168. Unique Substrings With Equal Digit Frequency (Premium)
6.2 Advanced
- 676. Implement Magic Dictionary
- 212. Word Search II
- 336. Palindrome Pairs
- 745. Prefix and Suffix Search
- 3093. Longest Common Suffix Query
- 3045. Count Prefix and Suffix Index Pairs II
- 1948. Delete Duplicate Folders in System
- 425. Word Squares (Premium)
- 527. Word Abbreviation (Premium)
- 588. Design In-Memory File System (Premium)
- 616. Add Bold Tag in String (Premium)
- 758. Bold Words in String (Premium)
- 642. Design Search Autocomplete System (Premium)
- 1065. Index Pairs of a String (Premium)
- 1166. Design File System (Premium)
- 1858. Longest Word With All Prefixes (Premium)
6.3 Trie Optimization with DP
- 139. Word Break
- 140. Word Break II
- 472. Concatenated Words
- 2977. Minimum Cost to Convert Strings II
6.4 0-1 Trie (XOR Trie)
Some problems can also be solved using guess-and-check methods.
- 421. Maximum XOR of Two Numbers in an Array
- 2935. Maximum XOR of Strong Number Pairs II
- 1707. Maximum XOR With an Element From Array
- 1803. Count Pairs With XOR in a Range
- 1938. Maximum Genetic Difference Query
- 2479. Maximum XOR of Two Non-Overlapping Subtrees (Premium)
Reference
https://leetcode.cn/problems/implement-trie-prefix-tree/solutions/2993894/cong-er-cha-shu-dao-er-shi-liu-cha-shu-p-xsj4/
https://leetcode.com/problems/implement-trie-prefix-tree/
https://leetcode.com/tag/trie/
https://www.bilibili.com/video/BV1Az4y1S7c7/?spm_id_from=333.999.0.0&vd_source=73e7d2c4251a7c9000b22d21b70f5635